堆的原理和实现

发表于   |   更新于 | 分类于 >
字数统计: 2.2k字 | 阅读时长 ≈ 9分钟

什么是堆

堆满足下面两点：

  • 是一颗完全二叉树
  • 大顶堆任意孩子节点小于或等于父节点(小顶堆任意孩子节点大于或等于父节点)

先来看几张图。
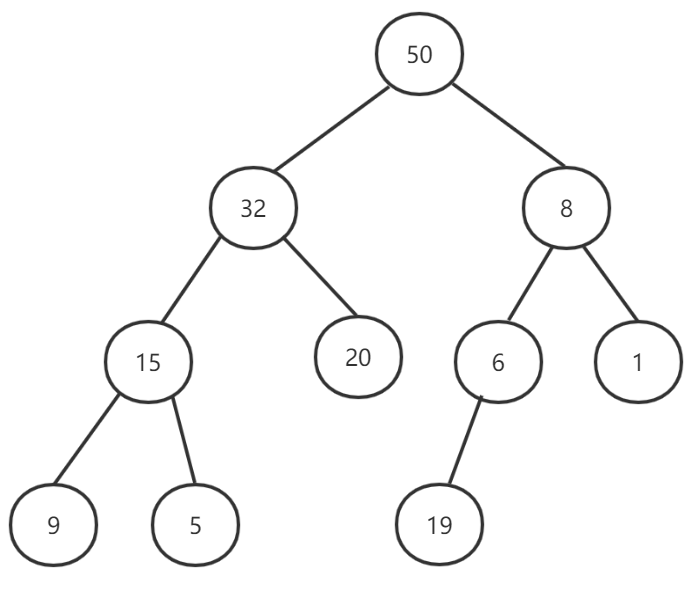
在这里插入图片描述

图1

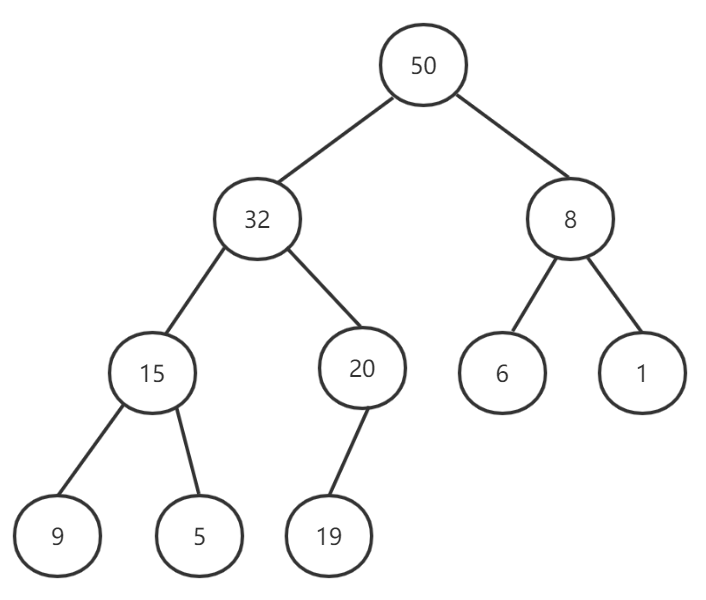
在这里插入图片描述

图2

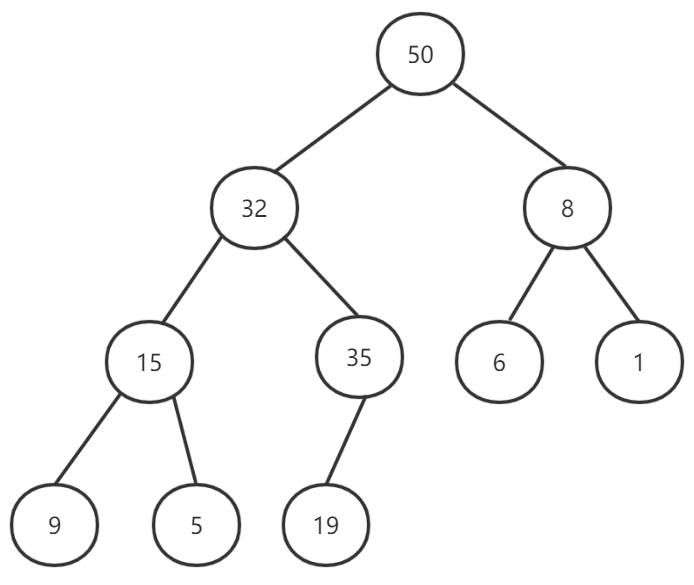
在这里插入图片描述

图3

上面几张图中，图1不满足完全二叉树的性质，图2是合格的最大堆，图3不满足孩子节点小于或等于父节点的性质。

堆的用途

优先队列指的是元素入队和出队的顺序与时间无关，既不是先进先出，也不是先进后出，而是根据元素的重要性来决定的。
例如，操作系统的任务执行是优先队列。一些情况下，会有新的任务进入，并且之前任务的重要性也会改变或者之前的任务被完成出队。而这个出队、入队的过程利用堆结构，时间复杂度是O($x^2$)。
注意：堆有很多种实现左式堆、斜堆、斐波那锲堆、二叉堆、三叉堆、N叉堆等。由于二叉堆使用很广泛，本文讨论的都是二叉堆。

堆的存储结构

由于数组占用的是连续的内存空间，相对来说对于散列存储的结构来说，数组可以节省连续的内存空间，不会将内存打乱，所以一般用数组存储堆的节点。
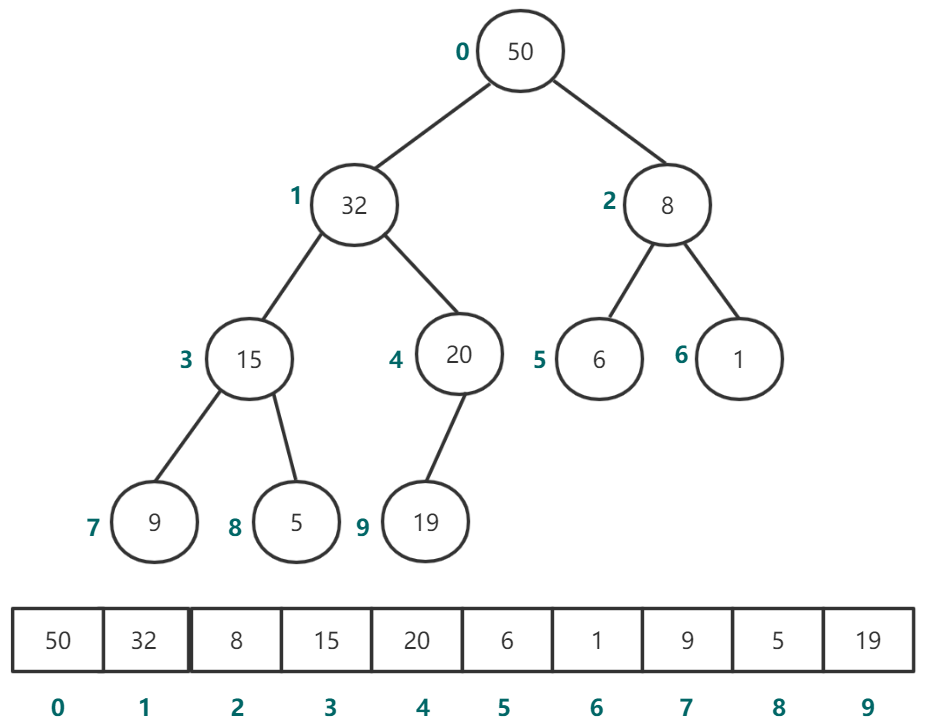
从数组下标0开始存储堆

图4 从数组下标0开始存储堆
图4是从数组下标0开始表示堆，可以看出对于堆中的父子节点关系：leftChild=2 * parent(i)+1、rightChild=2 * parent(i)+2、parent=(child(i)-1)/2。

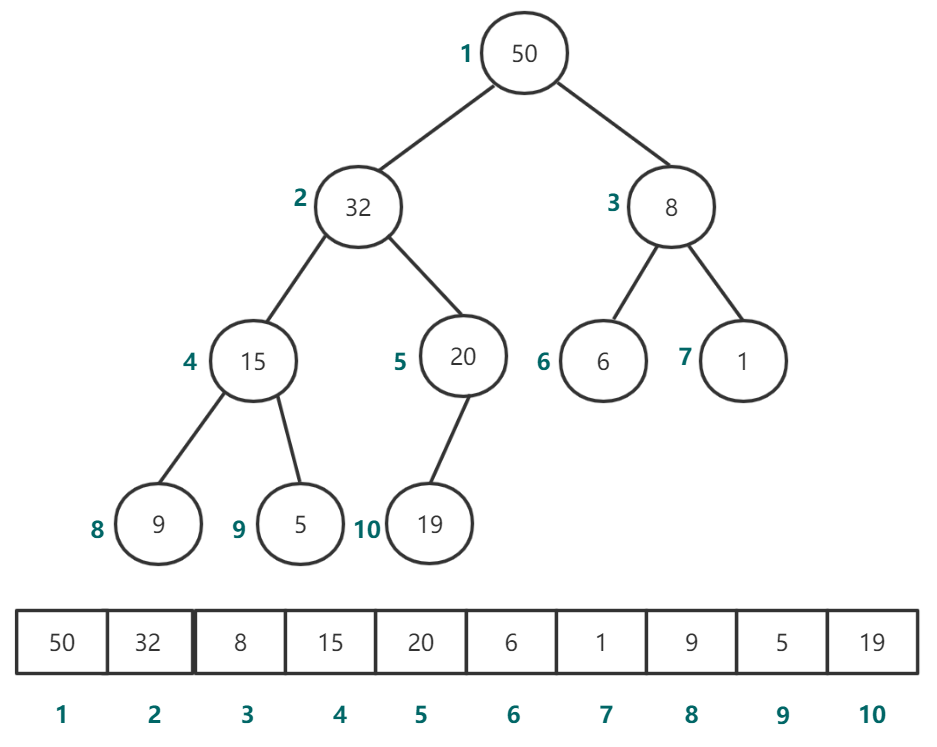
从数组下标1开始存储堆

图5 从数组下标1开始存储堆
图5是从数组下标1开始表示堆，可以看出对于堆中的父子节点关系：leftChild=2 * parent(i)、rightChild=2 * parent(i)+1、parent=child(i)/2。

一般情况下不选用下标为0的位置来存储数据，下标为0的位置通常使用一个很大的数字或者很小的数字作为哨兵变量,从下标1开始也能更方便地表示父子节点关系。本文后续的代码实现也是从1开始存储。

堆的基本操作(Java实现)

建堆

思路是将待建堆的数组当成一颗完全二叉树，然后从最后一个非叶子节点开始，和其孩子节点比较，依次向前循环非叶子节点保证堆序性，这个过程叫做下滤(percolate down)。从其存储结构知道parent=child(i)/2,那么最后一个非叶子节点=堆的大小/2。我们定义一个建堆数组和堆的大小，如下所示：

1
2
int[]  arr = {-1,19,20,32,5,45,6,8,9,15,1};  //-1为哨兵变量
int currentSize = arr.length - 1;//记录堆的大小，注意扩容操作

初始的完全二叉树如图6所示：
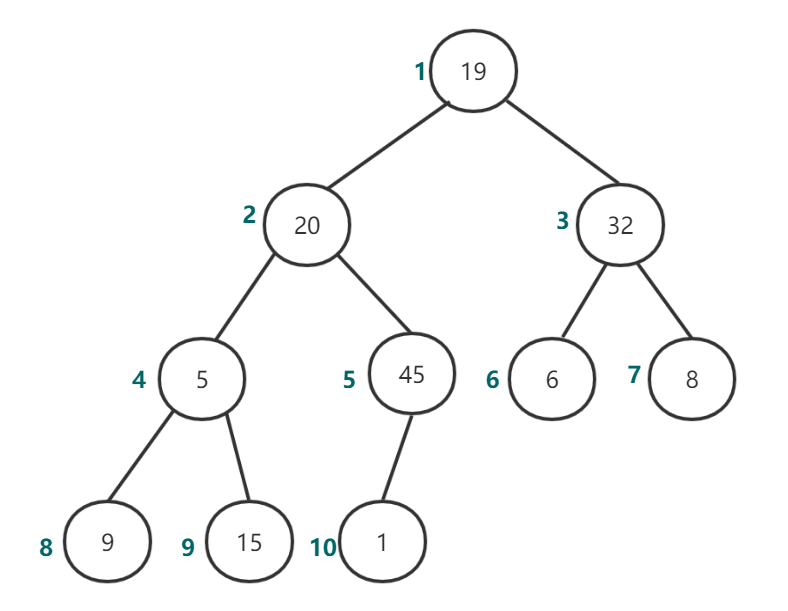
在这里插入图片描述

图6

进行percolateDown(5)后如图7所示：
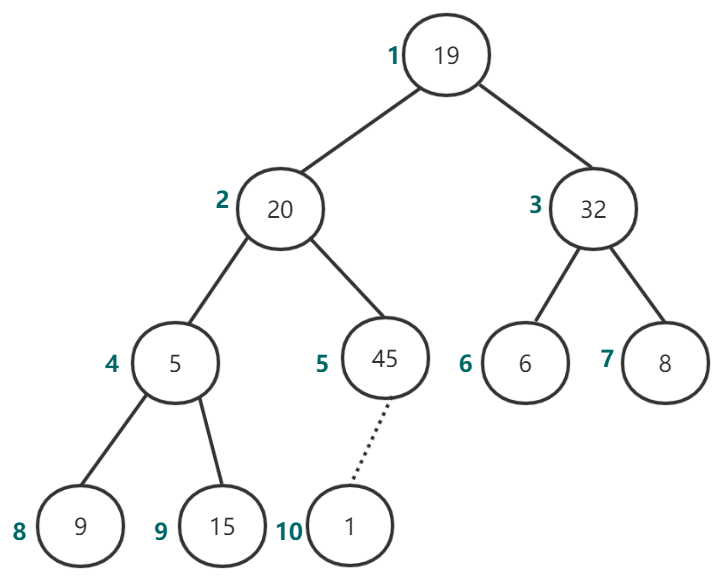
在这里插入图片描述

图7

进行percolateDown(4)后如图8所示：
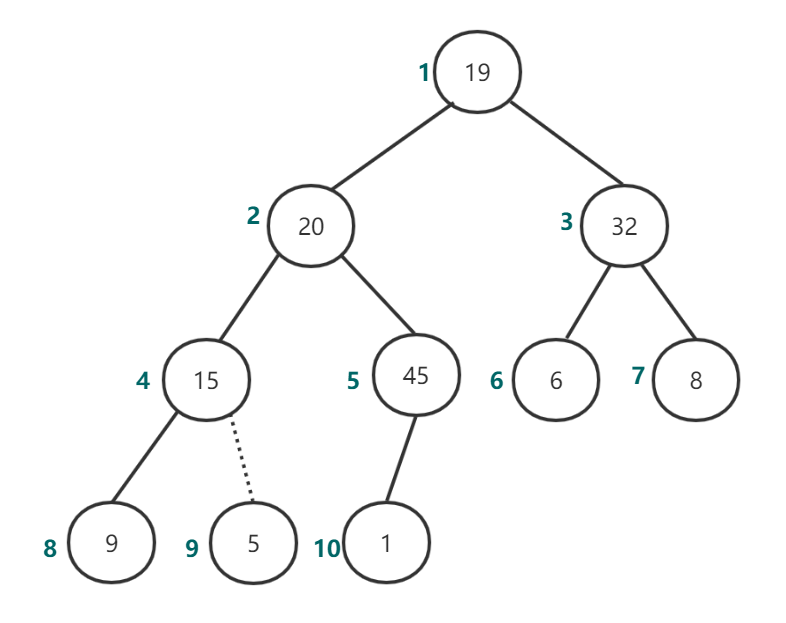
在这里插入图片描述

图8

进行percolateDown(3)后如图9所示：
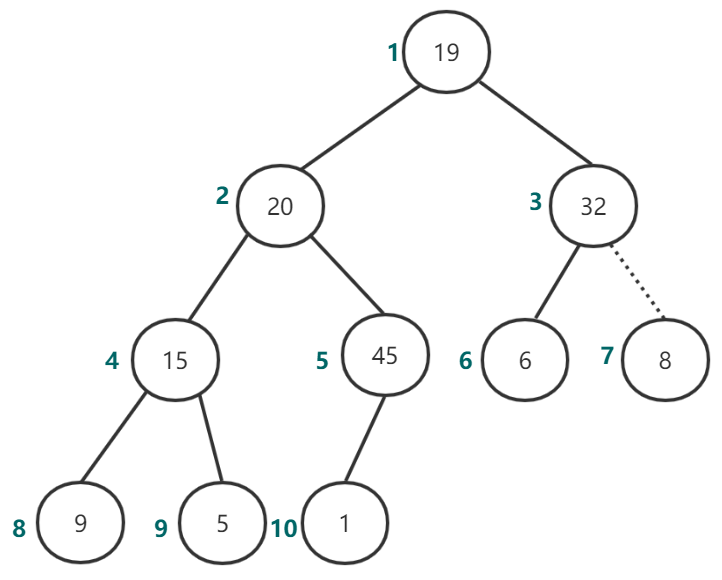
在这里插入图片描述

图9

进行percolateDown(2)后如图10所示：
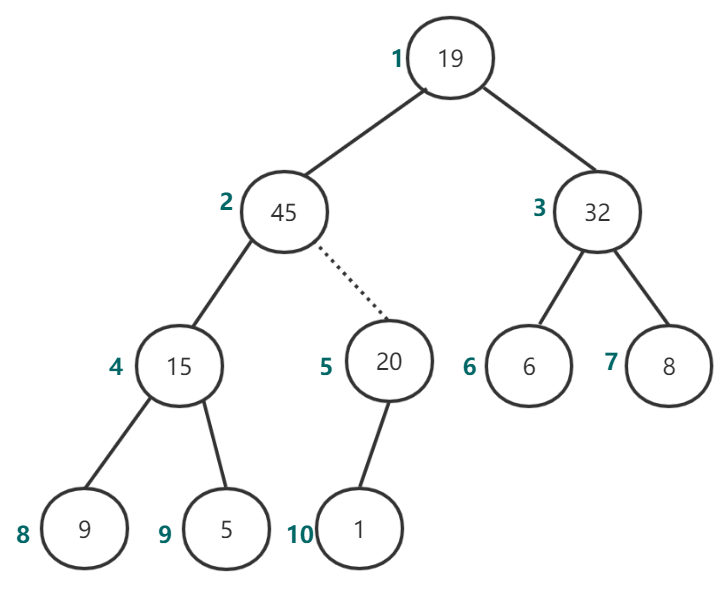
在这里插入图片描述

图10

进行percolateDown(1)后如图11所示：
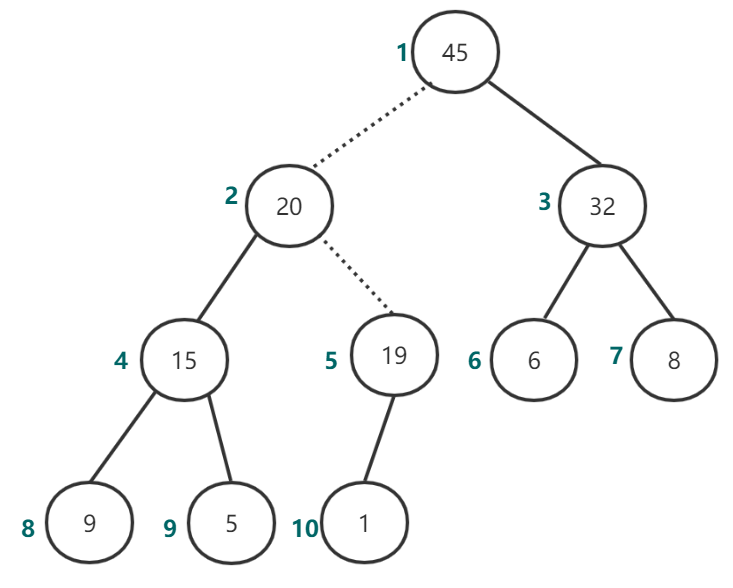
在这里插入图片描述

图11

这样一个二叉大顶堆就建好了。下滤操作的代码如下所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/**
  * 下滤操作
  * 保证每个非叶子节点都比其左右孩子大
  * @param i 待调整的节点(非叶子节点)
  * @param currentSize 堆的大小
  */
 private void percolateDown(int i, int currentSize) {
     int leftChild = i*2;
     int rightChild = leftChild+1;
     // 如果没有左孩子（越界），直接返回
     if (leftChild > currentSize) return;
     // 在左孩子与要调整的节点中找到最大的下标
     int maxIndex = arr[i] > arr[leftChild] ? i : leftChild;
     // 如果存在右孩子，在刚刚找到的最大的下标和右孩子中找最大的下标
     if (rightChild <= currentSize) maxIndex = arr[maxIndex] > arr[rightChild] ? maxIndex : rightChild;
     // 如果要调整的节点已经是最大的了，说明顺序正确，直接返回
     if (maxIndex == i) return;
     // 执行交换
     swapReferences(i, maxIndex);
     // 递归调整
     percolateDown(maxIndex, currentSize);
 }

建堆操作的代码如下所示：

1
2
for (int i = currentSize / 2; i >= 1; i--)
    percolateDown(i, currentSize);

删除堆顶元素

删除堆顶元素思路是用最后一个元素替换掉堆顶元素，堆的大小减1，再执行下滤(percolate down)操作调整。上面建好的堆删掉堆顶元素流程如下所示：
第一步，用最后一个元素替换堆，堆的大小减1。
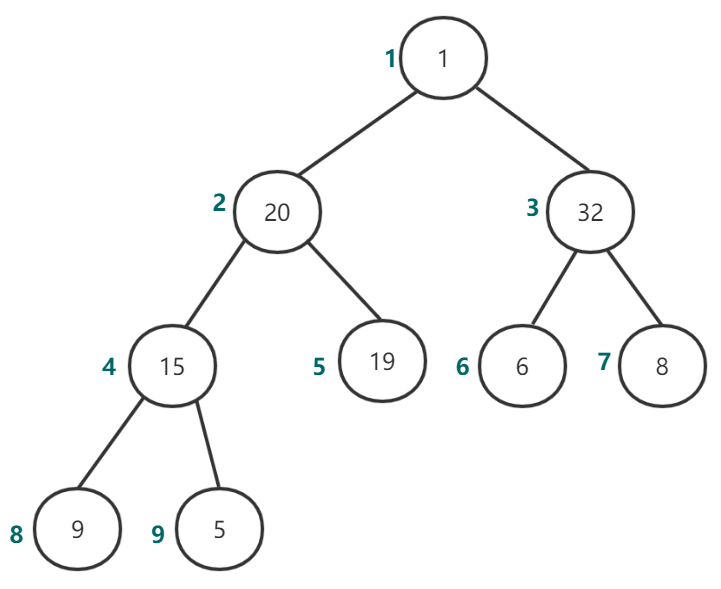
在这里插入图片描述

图12

第二步执行下滤操作，如图13-图14所示。
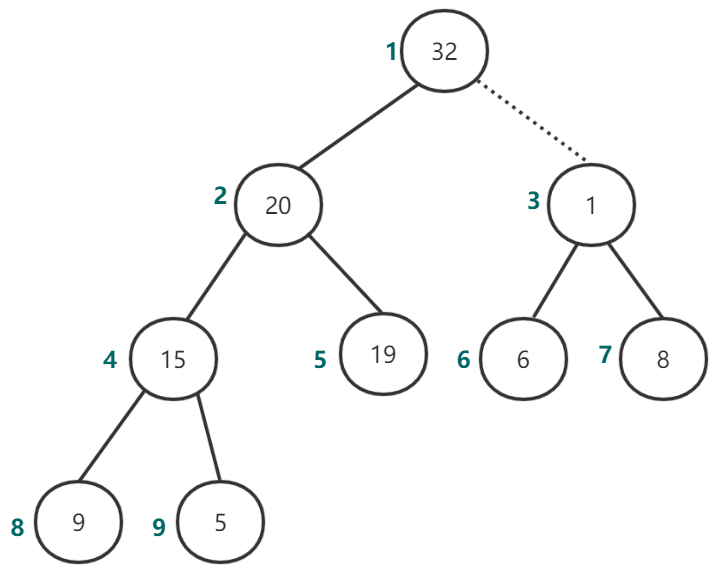
在这里插入图片描述

图13

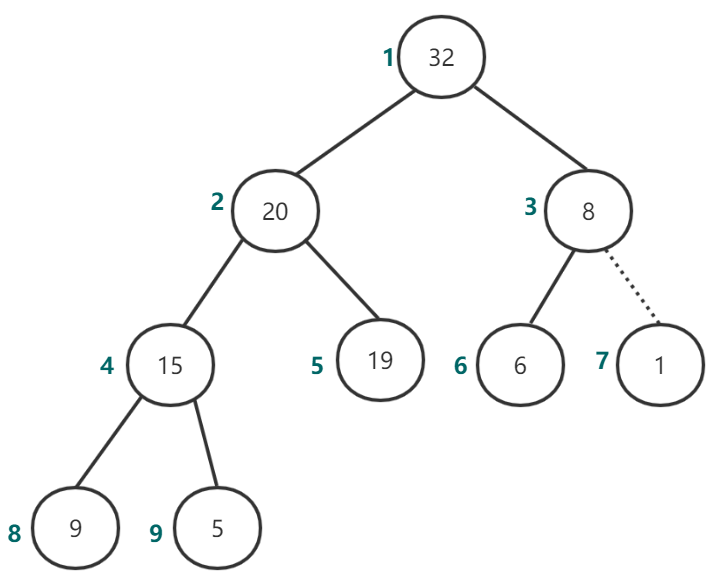
在这里插入图片描述

图14
这样顶部元素45就删除完成了。相关代码如下所示： 
1
2
3
// 用最后一个元素覆盖掉顶部的元素->堆元素个数减去1->执行下滤操作
arr[1] = arr[currentSize--];
percolateDown(1,currentSize);

插入

往堆中插入元素的思路是先把元素放到堆尾，然后循环和父节点比较大小，直到父节点比其大，这个过程叫做上滤(percolate up)。例如在上面的堆中插入50的过程如下所示：
第一步，把50放入堆尾，如图15所示。
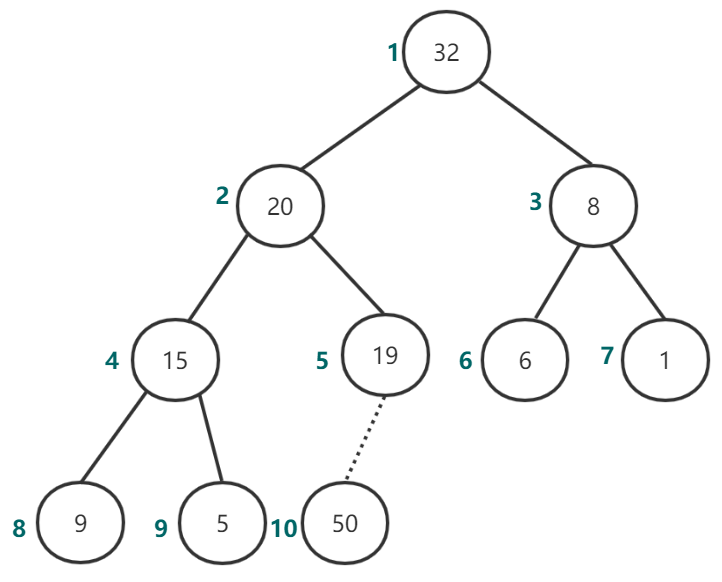
在这里插入图片描述

图15

第二步，执行上滤操作，如图16-18所示。
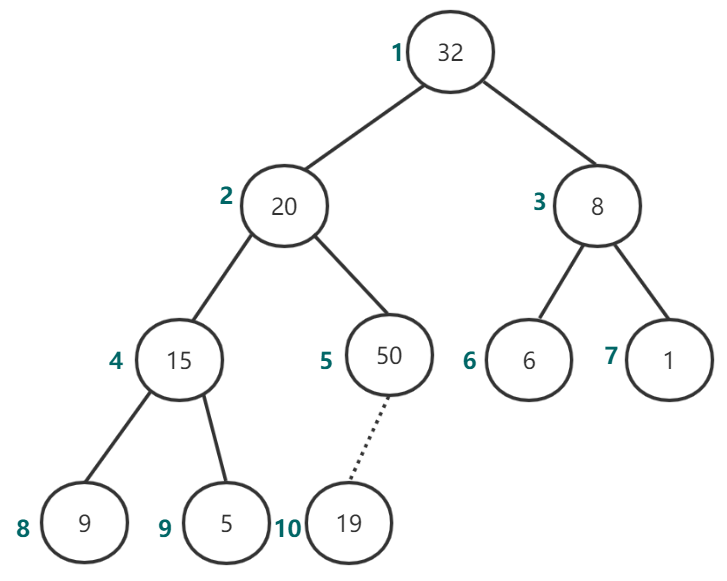
在这里插入图片描述

图16 执行上滤操作

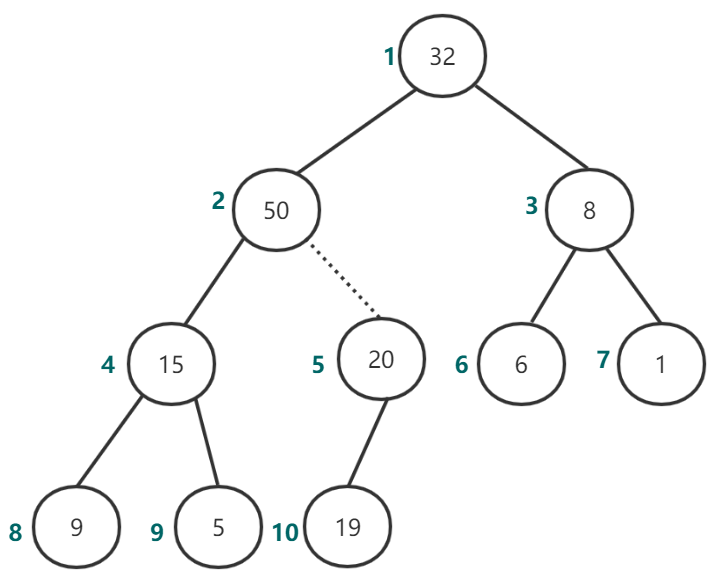
在这里插入图片描述

图17 执行上滤操作

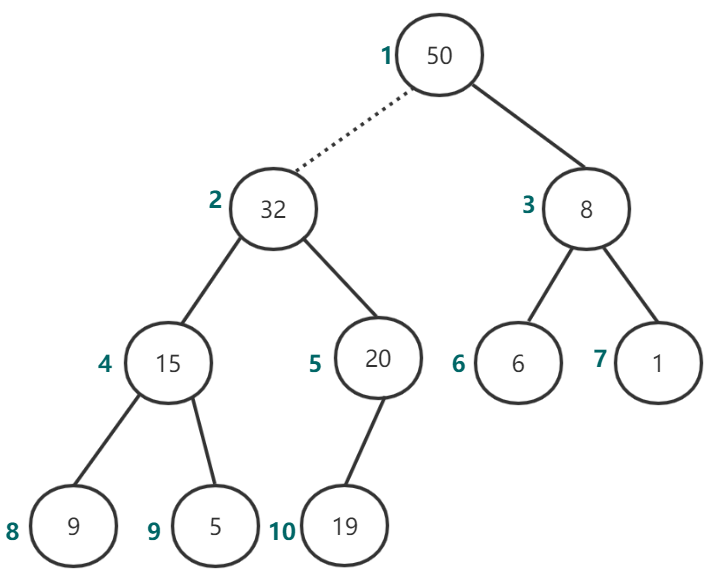
在这里插入图片描述

图18 执行上滤操作
上滤操作代码如下： 
1
2
3
4
5
6
7
8
9
10
11
12
13
/**
 * 上滤操作
 * 把每个叶子节点与其父节点进行比较，直到越界或者其父节点更大
 * @param i
 */
private void percolateUp(int i){
    int parent = i/2;
    if(parent < 1) return;
    if(arr[i] > arr[parent]){
        swapReferences(i,parent);
        percolateUp(parent);
    }
}

插入操作代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
/**
 * 堆操作：插入
 * 把元素插入到最后，然后递归执行上滤操作
 * @param x
 */
private void insert(int x){
    // 扩容
    if( currentSize == arr.length - 1 )
        enlargeArray(currentSize*2);
    arr[++currentSize]=x;
    percolateUp(currentSize);
}

完整源码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
package com.test;

import java.util.Arrays;

public class Heap {

 int[]  arr = {-1,19,20,32,5,45,6,8,9,15,1};  //-1为哨兵变量
 int currentSize = arr.length - 1;//记录堆的大小，注意扩容操作

 public static void main(String[] args) {
     Heap heap = new Heap();
     heap.bulidHeap();
 }

 /**
  * 堆操作：建立一个大顶堆
  * 从最后一个非叶子节点开始向前循环执行下滤操作
  */
 private void bulidHeap() {
     for (int i = currentSize / 2; i >= 1; i--)
         percolateDown(i, currentSize);
     System.out.println("建堆后结果：" + Arrays.toString(arr));
     System.out.println("当前堆大小："+currentSize);
 }

 /**
  * 下滤操作
  * 保证每个非叶子节点都比其左右孩子大
  * @param i 待调整的节点(非叶子节点)
  * @param currentSize 堆的大小
  */
 private void percolateDown(int i, int currentSize) {
     int leftChild = i*2;
     int rightChild = leftChild+1;
     // 如果没有左孩子（越界），直接返回
     if (leftChild > currentSize) return;
     // 在左孩子与要调整的节点中找到最大的下标
     int maxIndex = arr[i] > arr[leftChild] ? i : leftChild;
     // 如果存在右孩子，在刚刚找到的最大的下标和右孩子中找最大的下标
     if (rightChild <= currentSize) maxIndex = arr[maxIndex] > arr[rightChild] ? maxIndex : rightChild;
     // 如果要调整的节点已经是最大的了，说明顺序正确，直接返回
     if (maxIndex == i) return;
     // 执行交换
     swapReferences(i, maxIndex);
     // 递归调整
     percolateDown(maxIndex, currentSize);
 }

 /**
  * 交换数组元素
  * @param j 数组下标
  * @param i 数组下标
  */
 private void swapReferences(int j, int i) {
     int tmp = arr[j];
     arr[j] = arr[i];
     arr[i] = tmp;
 }

 /**
  *  堆操作：删除堆顶元素
  * 用最后一个元素覆盖掉顶部的元素->堆元素个数减去1->执行下滤操作
  * @return
  */
 private int deleteMax(){
     if(isEmpty()){
         System.out.println("当前堆已为空，不能删除！");
         return 0;
     }
     int max = arr[1];
     // 用最后一个元素覆盖掉顶部的元素->堆元素个数减去1->执行下滤操作
     arr[1] = arr[currentSize--];
     percolateDown(1,currentSize);

     arr = Arrays.copyOf(arr, currentSize+1);
     System.out.println("删除堆顶后结果：" + Arrays.toString(arr));
     System.out.println("当前堆大小："+currentSize);
     return max;
 }

 /**
  * 判空
  * 如果堆大小为0返回真
  * @return
  */
 private boolean isEmpty( )
 {
     return currentSize == 0;
 }

 /**
  * 堆操作：插入
  * 把元素插入到最后，然后递归执行上滤操作
  * @param x
  */
 private void insert(int x){
     // 扩容
     if( currentSize == arr.length - 1 )
         enlargeArray(currentSize*2);
     arr[++currentSize]=x;
     percolateUp(currentSize);
     System.out.println("插入"+x+"后结果：" + Arrays.toString(arr));
     System.out.println("当前堆大小："+currentSize);
 }

 /**
  * 扩容
  * @param newSize 新大小
  */
 private void enlargeArray(int newSize) {
     int [] old = arr;
     arr = new int[newSize];
     for( int i = 0; i<old.length; i++ )
         arr[i] = old[i];
 }

 /**
  * 上滤操作
  * 把每个叶子节点与其父节点进行比较，直到越界或者其父节点更大
  * @param i
  */
 private void percolateUp(int i){
     int parent = i/2;
     if(parent < 1) return;
     if(arr[i] > arr[parent]){
         swapReferences(i,parent);
         percolateUp(parent);
     }
 }
}

运行结果如下所示：

建堆后结果：[-1, 45, 20, 32, 15, 19, 6, 8, 9, 5, 1]
当前堆大小：10
删除堆顶后结果：[-1, 32, 20, 8, 15, 19, 6, 1, 9, 5]
当前堆大小：9
插入50后结果：[-1, 50, 32, 8, 15, 20, 6, 1, 9, 5, 19, 0, 0, 0, 0, 0, 0, 0]
当前堆大小：10

-------------本文结束感谢您的阅读-------------
失败是成功之母,打赏是成功支付